thing-a-week 37 and 38: Vedic square experiments

For weeks 37 and 38, I experimented with the Vedic square.

I've always admired the geometric designs in Islamic art and architecture but figured that the math involved would be too complicated to learn. But, another recent Good Job Brain episode unlocked at least one secret for me by telling me about the Vedic square.

You can go ahead and read the brief Wikipedia article article about it, but the Vedic square is a 9x9 table that shows digital roots — the remainder of ((x * y) / 9) — instead of multiplication products:

Thanks, Wikipedia.

If you draw lines connecting all the same digital roots in the square, you can already make some pretty neat shapes.

But you can also make simple, elegant designs if you take a whole row from the square, use the numbers in that row as measurements, and keep turning your paper at a certain angle until you get back to where you started.

Of course, those instructions might be difficult to understand without an example, but I'll get to those in a bit; please bear with my nerding out a little longer.

I tried to go all pen-and-paper for this, but it turns out that my protractor is inexact, so I put these black-and-white drawings together on a computer. Even then, I had trouble getting everything to line up just right, so I really have to hand it to the first artists who worked with these measurements by hand.

Whatever angle you choose, it looks like you'll get yourself nine possible shapes. I first went with all 90-degree angles, and all but one row led me to produce these swastika-like shapes. This is the one with sequence 1 (1, 2, 3, … , 9):

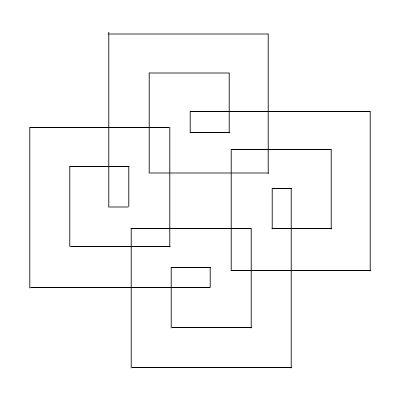
Sequence 5 (5, 1, 6, 2, 7, 3, 8, 4, 9):

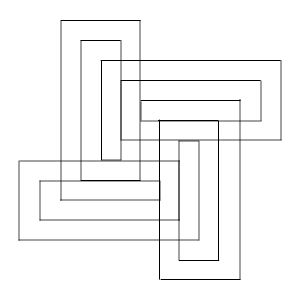
Sequence 7 (7, 5, 3, 1, 8, 6, 4, 2, 9):

Sequences 2, 4, and 8 produced the same patterns, but in the reverse direction. Sequences 3 and 6, I felt, were too simple — four connected or overlapping rectangles in the same turning shape. The one row that didn't produce such a shape was row 9, which gave only a square.

At this point, I could appreciate for myself how the numbers of the Vedic square could be kind of cosmic, or why people might see them as holy, magical, or divine. The sequences are so simple, but if you follow them with one unbroken line, you create a shape that turns forever, and you always end up back where you began.

If you think this says something about the nature of life and the universe, then you'll probably find this either depressing or comforting.

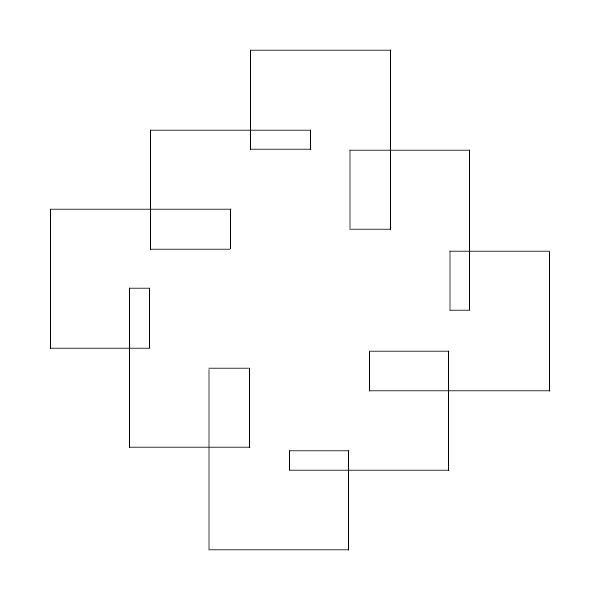
I did two more designs by turning at a 45-degree angle. Here's sequence 2:

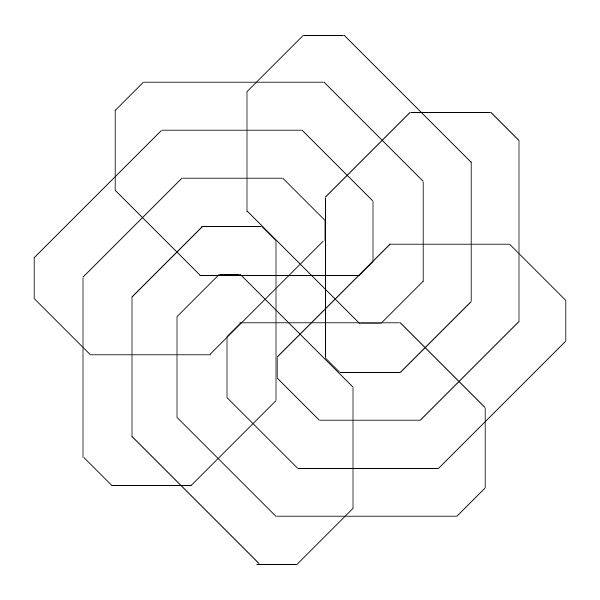
and sequence 5:

Of course, these things just beg to be colored, so I also printed out this last one and used it as a template for this:

To my frustration, of course, doing this with paper wasn't as neat as it was on the computer. But, I like it enough to want to make more. And I still have other angles to try.